.
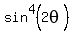 -
- 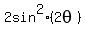 = -1 <====> (is equivalent to)
= -1 <====> (is equivalent to)
 = 0 <====> (is equivalent to)
= 0 <====> (is equivalent to)
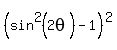 = 0 <====> (is equivalent to)
= 0 <====> (is equivalent to)
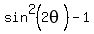 = 0 <====> (is equivalent to)
= 0 <====> (is equivalent to)
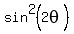 = 1 <====> (is equivalent to)
= 1 <====> (is equivalent to)
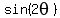 = +/- 1.
Case 1.
= +/- 1.
Case 1. 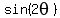 = 1 is equivalent to
= 1 is equivalent to 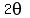 =
=  ,
,  ,
,  , . . . ,
, . . . , 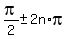 , where n is any integer.
General solution for this case is
, where n is any integer.
General solution for this case is  =
= 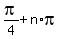 , where n is any integer.
Case 2.
, where n is any integer.
Case 2. 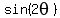 = -1 is equivalent to
= -1 is equivalent to 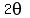 =
= 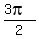 ,
,  ,
, 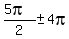 , . . . ,
, . . . , 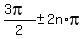 , where n is any integer.
General solution for this case is
, where n is any integer.
General solution for this case is  =
= 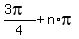 , where n is any integer
Answer. Any angle of the set
, where n is any integer
Answer. Any angle of the set 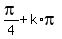 ,
, 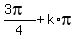 is the solution, where k is any integer.
is the solution, where k is any integer.
====================
One and only one question per post, PLEASE.
It is the policy, the rule and the requirement of this forum.