Question 1122750: Write an equation in slope-intercept form for the line described.
x-intercept -5, y-intercept 8
Find an equation for the line which passes through (-2,3) and is perpendicular to the line containing (0,3) and (3,6).
Find an equation of the line having the given slope and containing the given point.
m = 4/5, (6,-6)
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! y=mx+b, m is slope and b the y-value of the y-intercept (x=0)
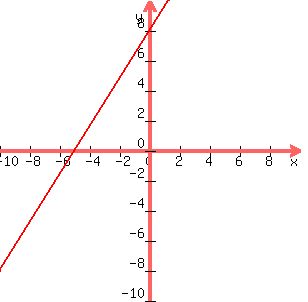
slope goes between points (-5, 0) and (0, 8), and that is a slope of (8-0)/0-(-5)) or 8/5
y=(8/5)x+8
perpendicular lines have product of slopes = -1
line given has slope of 3/3 or 1
line desired has slope of -1
point slope formula y-y1=m(x-x1), m slope and (x1, y1) point
Line containing (0, 3) and (3, 6) can be plotted to show y=x+3
perpendicular line has slope -1
point slope formula y-y1=m(x-x1), m slope and (x1, y1) point
y-3=(-1)(x+2)
y=-x+1

point slope formula y-y1=m(x-x1), m slope and (x1, y1) point
y+6=(4/5)(x-6)
y+6=(4/5)x-(24/5)
y=(4/5)x-(54/5)
|
|
|