Question 1122463: A theater has a seating capacity of 1050 and charges $3 for children, $5 for students, and $7 for adults. At a certain screening with full attendance, there were half as many adults as children and students combined. The receipts totaled $5150. How many children attended the show?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52904)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A theater has a seating capacity of 1050 and charges $3 for children, $5 for students, and $7 for adults.
At a certain screening with full attendance, there were half as many adults as children and students combined.
The receipts totaled $5150. How many children attended the show?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by @josgarithmetic was WRONG starting from his very first equation,
so I came with the correct solution.
For your safety, simply ignore writing by @josgarithmetic.
Let x =# of children, y = # of students and z = # of adults.
Then you have this two equation
x + y + z = 1050 (1) (the total) and
z = 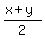 (2) ("there were half as many adults as children and students combined.")
Substitute eq(2) into eq(1), replacing z. You will get
x + y + (2) ("there were half as many adults as children and students combined.")
Substitute eq(2) into eq(1), replacing z. You will get
x + y +  = 1050, or = 1050, or
 = 1050, which gives you
x + y = = 1050, which gives you
x + y = 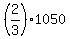 = 700.
So, you know now that the combined number of children and students was 700.
You also know that the number of adults was 1050 - 700 = 350.
So, adults payed 350*7 = 2450 dollars;
then children and students payed 5150 - 2450 = 2700 dollars for their tickets.
Now you have this system of 2 equations in 2 unknowns
x + y = 700, (2)
3x + 5y = 2700. (3)
Thus you reduced the original problem from 3 unknowns to only 2 unknowns
Now solve the system (2),(3) by substitution method. From eq(1) express y = 700 - x and substitute it into eq(2). You will get
3x + 5*(700-x) = 2700
3x - 5x = 2700 - 3500
-2x = -800 ====> x = 400.
The number of children was 400; the number of students was 700-400 = 300; the number of adults was 350. = 700.
So, you know now that the combined number of children and students was 700.
You also know that the number of adults was 1050 - 700 = 350.
So, adults payed 350*7 = 2450 dollars;
then children and students payed 5150 - 2450 = 2700 dollars for their tickets.
Now you have this system of 2 equations in 2 unknowns
x + y = 700, (2)
3x + 5y = 2700. (3)
Thus you reduced the original problem from 3 unknowns to only 2 unknowns
Now solve the system (2),(3) by substitution method. From eq(1) express y = 700 - x and substitute it into eq(2). You will get
3x + 5*(700-x) = 2700
3x - 5x = 2700 - 3500
-2x = -800 ====> x = 400.
The number of children was 400; the number of students was 700-400 = 300; the number of adults was 350.
Solved.
|
|
|