SOLUTION: How many ways can a team of fifteen hockey players choose a captain and two alternate captains?

Algebra ->  Permutations -> SOLUTION: How many ways can a team of fifteen hockey players choose a captain and two alternate captains?      Log On


   

Question 1122451: How many ways can a team of fifteen hockey players choose a captain and two alternate captains?
Answer by ikleyn(52784) About Me  (Show Source):
You can put this solution on YOUR website!
.
The captain is a UNIQUE and DISTINGUISHABLE position.


It can be chosen in 15 ways.



Two alternate captains are two indistinguishable positions, so we use COMBINATIONS in this case,

and the number of relevant combinations is 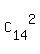 C%5B14%5D%5E2 = %2814%2A13%29%2F2 = 91 ways.



So the answer to the problem's question is THIS :  in  15*91 = 1365 ways.

Solved.