Question 1122329: Given that the modulus of the complex number |z+1+2i|=3, find the maximum and minimum values of |z-3+i|
Found 2 solutions by Alex.33, ikleyn:
Answer by Alex.33(110)   (Show Source):
You can put this solution on YOUR website! Grab a pencil and blank paper if you can or do it in your imagination.
We now have a complex number(z+1+2i), it's magnitude is 3. So we draw a circle with radius 3 and center on (0,0), on the complex plane. This represents the endpoints of all possible complex number(z+1+2i)s.
To get the endpoint of (z-3+i), we must add (z+1+2i) with (-4-i), which means we must move its endpoint 4 units in the negative imaginary axis' direction and 1 in the nagative real axis' direction. Try do it with random endpoints in the circle-which one gives the longest magnitude(distance to the origin) and smallest?
You'll see the answer is pretty simple. The maximum and minimum magnitude both occur when the endpoints of (z+1+2i) are on the line which (-4-i) is on. Now time for calculations.
Maximum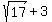 
Minimum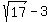 
Answer by ikleyn(52810)  (Show Source):
You can put this solution on YOUR website! .
The equation |z+1+2i| = 3 represents the set of points in the complex plane that are remoted in 3 units from the point (-1,-2).
It is the circle of the radius 3 with the center at the point (-1,-2).
So the problem asks to find the minimum and the maximum distance from the point (3,-1) to this circle.
The distance from the center of the circle (-1,-2) to the point (3,-1) is
 =  =  .
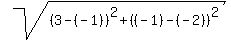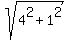This distance is greater than 3, so the point (3,-1) lies outside that circle.
Now, it is very simple to find the maximum distance and the minimum distance from the given point to the circle.
Simply connect the center (-1,-2) with the point (3,-1) by the straight line.
The minimum will be -3; the maximum will be + 3.
|
|
|
