Question 1122267: The total number of passengers riding a certain city bus during the morning shift is 1100. If the child's fare is $0.50, the adult fare is $1.50, and the total revenue from the fares in the morning shift is $1350, how many children and how many adults rode the bus during the morning shift?
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source):
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
Let assume for a minute that all 1100 passengers in this morning were children.
Then the revenue would be 1100*$050 = $550, making shortage of $1350 - $550 = $800.
The shortage is due to the fact that we counted all 1100 tickets as children tickets.
To compensate the shortage, we should replace some number of children tickets in our counting by adults tickets.
At every such replacement, we diminish the shortage of $800 by $1.00 = $1.50 - $0.50.
So, the number of such replacements is the ratio 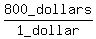 = 800.
Hence, the correct number of adult tickets is 800.
Then the number of the children tickets is the rest of 1100 - 800 = 300.
Answer. 800 adults and 300 children.
Check. 800*$150 + 300*$0.50 = $1350. ! Correct !
Solved (quickly and mentally, without using equations).
--------------------
On solving ticket problems see the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
The total number of passengers riding a certain city bus during the morning shift is 1100. If the child's fare is $0.50, the adult fare is $1.50, and the total revenue from the fares in the morning shift is $1350, how many children and how many adults rode the bus during the morning shift?
Let number of adults be A
Then number of children = 1,100 - A
We then get: 1.5A + .5(1,100 - A) = 1,350
1.5A + 550 - .5A = 1,350
1.5A - .5A = 1,350 - 550
A, or number of adults = 
Subtract 800 from 1,100 to get the number of children!
That's all!! Nothing more, nothing LESS! That's how SIMPLE this is!
|
|
|
