You can
put this solution on YOUR website! .
Let the smallest angle is x degrees and the largest is y degrees.
The sum of all four interior angles of a quadrilateral is 360 degrees.
Since four angles form arithmetic progression, the formula for their sum is
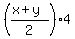 = 360, which implies
x + y = 180. (1)
The second equation is
y = 2x + 15. (2)
Substitute eq(2) into eq(1). You will get
x + (2x+15) = 180,
3x = 180 - 15 = 165 ====> x =
= 360, which implies
x + y = 180. (1)
The second equation is
y = 2x + 15. (2)
Substitute eq(2) into eq(1). You will get
x + (2x+15) = 180,
3x = 180 - 15 = 165 ====> x =  = 55.
Answer. The smallest angle is 55 degrees. The greatest angle is 2x + 15 = 2*55 + 15 = 110 + 15 = 125 degrees.
= 55.
Answer. The smallest angle is 55 degrees. The greatest angle is 2x + 15 = 2*55 + 15 = 110 + 15 = 125 degrees.
Solved.