You can
put this solution on YOUR website! .
(cos(6x) + 6cos(4x) + 15cos(2x) + 10)/(cos(5x) + 5cos(3x) + 10cos(x))
Consider the numerator and re-group it in this way
Numerator = cos(6x) + 6*cos(4x) + 15*cos(2x) + 10 =
= (cos(6x) + cos(4x)) + (5*cos(4x) + 5*cos(2x)) + (10*cos(2x) + 10) (*)
Next, use the basic Trigonometry formula cos(a) + cos(b) = 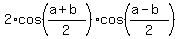 . You will get
cos(6x) + cos(4x) = 2*cos(5x)*cos(x),
cos(4x) + cos(2x) = 2*cos(3x)*cos(x),
cos(2x) + 1 = 2*cos(x)*cos(x).
Substitute it into the formula (*). Then you can continue (*) in this way
Numerator = 2*cos(5x)*cos(x) + 5*2*cos(3x)*cos(x) + 10*2*cos(x)*cos(x) =
= 2*cos(x)*(cos(5x) + 5*cos(3x) + 10*cos(x))
Now notice that the long expression in the Numerator parentheses is exactly the denominator of the original formula.
Canceling common factors in the numerator and denominator, you get the final expression
(cos(6x) + 6*cos(4x) + 15*cos(2x) + 10) / (cos(5x) + 5*cos(3x) + 10*cos(x)) = 2*cos(x)
Answer. (cos(6x) + 6*cos(4x) + 15*cos(2x) + 10) / (cos(5x) + 5*cos(3x) + 10*cos(x)) = 2*cos(x).
. You will get
cos(6x) + cos(4x) = 2*cos(5x)*cos(x),
cos(4x) + cos(2x) = 2*cos(3x)*cos(x),
cos(2x) + 1 = 2*cos(x)*cos(x).
Substitute it into the formula (*). Then you can continue (*) in this way
Numerator = 2*cos(5x)*cos(x) + 5*2*cos(3x)*cos(x) + 10*2*cos(x)*cos(x) =
= 2*cos(x)*(cos(5x) + 5*cos(3x) + 10*cos(x))
Now notice that the long expression in the Numerator parentheses is exactly the denominator of the original formula.
Canceling common factors in the numerator and denominator, you get the final expression
(cos(6x) + 6*cos(4x) + 15*cos(2x) + 10) / (cos(5x) + 5*cos(3x) + 10*cos(x)) = 2*cos(x)
Answer. (cos(6x) + 6*cos(4x) + 15*cos(2x) + 10) / (cos(5x) + 5*cos(3x) + 10*cos(x)) = 2*cos(x).