Question 1122116: I need your help on the following:
A. A child chosen at random in a community school system comes from a low-income family 15 percent of the time. Children from low-income families in the community graduate from college only 20 percent of the time. Children not from low-income families have a 40 percent chance of graduating from college. As an employer of people from this community, you are reviewing applicants and note that the first one had a college degree. What is the probability that the person comes from low-income family?
B. By very carefully screening applicants, the Bank of Halifax Country has been able to limit bad-debt losses on consumer loans to 8 percent. What is the probability that at least four of the five loan applicants that you, as a loan officer trainee, have just approved will repay their loans?
Found 3 solutions by rothauserc, ikleyn, greenestamps:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! A) 15% come from low income family, low income students graduate college 20% of the time
:
multiply the two probabilities
:
0.15 * 0.20 = 0.03
:
Probability(P) that the person comes from low-income family is 3%
:
B) A loan has a 100-8 = 92% P of repaying after screening
:
P that at least four of the five loan applicants repay = P(4 repay out of 5) +P(5 repay out of 5)
:
we can use the binomial P formula since the screening is the same for each application
:
P(k successes out n trials) = nCk * p^k * (1-p)^(n-k), where nCk = n!/(k!*(n-k)!)
:
P(4 repay out of 5) = 0.2866
:
P(5 repay out of 5) = 0.6591
:
P(at least four of the five loan applicants repay) = 0.2866 + 0.6591 = 0.9457 approximately 95%
:
Answer by ikleyn(52894)  (Show Source):
You can put this solution on YOUR website! .
I came to fix the solution to Problem A given by the tutor @rothauserc, which is wrong.
We have to interpret the condition in this way:
15% of children in a community school system come from low-income families
and the rest 100%-15% = 85% come from not low-income families.
Now, the problem asks what is the probability that the applicant having a college degree comes from a low income family.
It is the "conditional" probability.
So the solution is
the probability under the question is 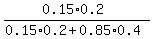 = 0.081081 = 8.1% (approximately).
The denominator is the probability that the applicant has a college degree.
Solved.
Answer by greenestamps(13209)  (Show Source):
You can put this solution on YOUR website!
Addressing question A again, to confirm the solution by tutor @ikleyn....
This is conditional probability. We are to find the probability that a child comes from a low income family, GIVEN THAT the child has a college degree.
So the numerator of the probability fraction is all the children from low income families that have a college degree. 15% of the children are from low income families; and 20% of the children from low income families have college degrees. So the numerator is 20% of 15%: (0.20)(0.15) = 0.03.
The denominator of the probability fraction is ALL the children who have a college degree. That is 40% of the 85% of children who are not from low income families and 20% of the 15% of the children who are: (0.40)(0.85)+(0.20)(0.15) = 0.34+0.03 = 0.37.
So the probability that the question asks for is 0.03/0.37 = 0.081 or about 8.1%.
|
|
|
