SOLUTION: Pease help me solve this equation: Find the dimensions of a rectangle whose area is 247 cm2 and whose perimeter is 64 cm. (Enter your answers as a comma-separated list.)

You are given that the perimeter of the rectangle is 64 cm;  hence, the sum of the length and the width is one half of that:

x + y = 32,  where x is the length, and y is the width.


Then the average of the length and the width is one half of 32, i.e. 16.


It is clear that the values of x and y are remoted at the same value/distance "u" from 16, so we can write

x = 16 + u,
y = 16 - u.


Then the area is  xy = (16+u)*(16-u) = 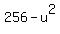, and it is equal to 247, according to the condition.

Hence,   = 247,  which gives   = 256 - 247 = 9,  and then  u =  = 3.


Thus the length is  x = 16 + u = 16 + 3 = 19,

and  the width  is  x = 16 - u = 16 - 3 = 13.


Answer.  The dimensions of the rectangle are  13 cm  and  19 cm.