Question 112182: I am given three points on a graph (14,0), (10.5,1), (6.5,3) and am asked to find the equation for the parabola that passes through these points. I understand that the parabola must be positive and open upwards. Also, I know that the "c" value must be 14 because that is the y intercept. But, from then on, I really have no idea what to do. Could you please help me?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am given three points on a graph (14,0), (10.5,1), (6.5,3) and am asked to find the equation for the parabola that passes through these points. I understand that the parabola must be positive and open upwards. Also, I know that the "c" value must be 14 because that is the y intercept. But, from then on, I really have no idea what to do. Could you please help me?
The c value is not what you thought.
You were thinking (14,0) was (0,14)
but it's just backwards from that.
Here we go from scratch:
A quadratic function has a parabola for its graph and
it must have an equation of thge form:
y = ax² + bx + c
So plug each of the points in that equation.
Plug in (x,y) = (14,0)
y = ax² + bx + c
0 = a(14)² + b(14) + c
0 = 196a + 14b + c
-------
Plug in (x,y) = (10.5,1)
y = ax² + bx + c
1 = a(10.5)² + b(10.5) + c
1 = 110.25a + 10.5b + c
-------
Plug in (x,y) = (6.5,3)
y = ax² + bx + c
3 = a(6.5)² + b(6.5) + c
3 = 42.25a + 6.5b + c
-------
So we have this system
0 = 196a + 14b + c
1 = 110.25a + 10.5b + c
3 = 42.25a + 6.5b + c
or, putting the numbers on the right and lining up
the letters:
196a + 14b + c = 0
110.25a + 10.5b + c = 1
42.25a + 6.5b + c = 3
Can you solve that system? If not post again.
The answers to that system are a = 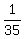 , b = , b = 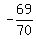 , c = , c =  So y = ax² + bx + c becomes
y =
So y = ax² + bx + c becomes
y = 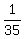 x² - x² - x + x +  It has vertex (
It has vertex (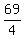 , , 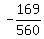 )
Its x-intercepts are (14, 0) and (41/2, 0)
Its y intercept is (0, 41/5)
Its axis of symmetry has the equation x = )
Its x-intercepts are (14, 0) and (41/2, 0)
Its y intercept is (0, 41/5)
Its axis of symmetry has the equation x = 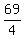 Its graph is this with the green line as the
axis of symmetry:
Its graph is this with the green line as the
axis of symmetry:
 Edwin
Edwin
|
|
|