|
Question 1121661: In an examination,53% students passed in maths,61% passrd in physics,60% passed in chemistry,24% passed in maths and physics,35% passed in physics and chemistry,27% passed in maths and chemistry and 5% in none. The ratio of percentage of passes in maths and chemistry but not in physics.In relation to percentage of passes in physics and chemistry but not in maths is?
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When you solve such problems, the key to success is to introduce compact abbreviations (notations) that work.
Let M be the set (and at the same time the percentage) of those who passed Math (53%)
P ------------------------------- " --------------------------------- Physics (61%)
C ------------------------------- " --------------------------------- Chemistry (60%)
MP ------------------------------ " --------------------------------- Math and Physics (24%)
PC ------------------------------ " --------------------------------- Physics and Chemistry (35%)
MC ------------------------------ " --------------------------------- Math and Chemistry (27%)
N ------------------------------- " --------------------------------- in none
This "none" I interpret in a way that these 5% are not included to either of the categories above and complement the set to 100%.
Then the only unknown is the intersection MPC of the three sets M, P and C.
It is easy to find the measure (the percentage) of MPC.
From the elementary set theory we have this equation
100% = 5% + M + P + C - MP - PC - MC + MPC, (*)
which gives you
MPC = 100 - 5 - 53 - 61 - 60 + 24 + 36 + 37 = 18%.
Now, in the ratio you want to get, the numerator is MC - MPC = 27% - 18% = 9%;
the denominator is PC - MPC = 35% - 18% = 17%.
Therefore, the ratio under the question is equal to 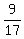 . .
Solved.
---------------
Regarding the formula (*) see the lesson
- Advanced problems on counting elements in sub-sets of a given finite set
in this site.
|
|
|
| |