SOLUTION: Hello I need some help on this question, it says Draw theta= 67pi/12 in standard position and to name a reference angle to theta. I know the unit circle and the fundamental

Algebra ->  Trigonometry-basics -> SOLUTION: Hello I need some help on this question, it says Draw theta= 67pi/12 in standard position and to name a reference angle to theta. I know the unit circle and the fundamental      Log On


   

Question 1121656: Hello I need some help on this question, it says
Draw theta= 67pi/12 in standard position and to name a reference angle to theta.
I know the unit circle and the fundamental radians but I’m having trouble trying to find 67pi/12. Is there a good way to go about this or do I subtract radians from 67pi/12? Any help to understand this would really help, thank you!

Answer by ikleyn(52794) About Me  (Show Source):
You can put this solution on YOUR website!
.

I will help you to make your problem easier. 


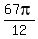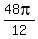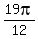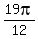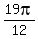    67pi%2F12 = 48pi%2F12 + 19pi%2F12 = 4pi + 19pi%2F12.


4pi is two complete rotations, and geometrically it is the same as the angle of zero radians.


So, your original angle is equivalent to (is the same as)  19pi%2F12 = pi + 7pi%2F12.


Now, if you, as you said, know the unit circle, you can complete the assignment on your own.


The lesson to learn from this solution : 

     When it is needed, extract the integer number of full rotations, i.e. the angle multiple of 2pi.