Question 1121450: a) Expand and simplify (x+y)(x^2-xy+y^2)
b) If x+y = 1 and x^3 +y^3 = 19, find the values of x^2+y^2
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! x^3-x^2y+xy^2+x^2y-xy^2+y^3
=x^3+y^3, and the factors can lead one to this result directly.
x^2-xy+y^2=19, since x+y=1
y=1-x
so x^2-x(1-x)+1-2x+x^2=19
x^2-x+x^2+1-2x+x^2=19
3x^2-3x=18
x^2-x-6=0
(x-3)(x+2)=0
x=3 (and y=-2)
x=2 (and y=-3)
x^2+y^2=13 ANSWER
Answer by ikleyn(52914)  (Show Source):
You can put this solution on YOUR website! .
a) Expand and simplify (x+y)(x^2-xy+y^2)
b) If x+y = 1 and x^3 +y^3 = 19, find the values of x^2+y^2
~~~~~~~~~~~~~~~~~~~~~~~
a) Expand and simplify (x+y)(x^2-xy+y^2)
(x+y)(x^2-xy+y^2) = x^3 + y^3.
It is the standard and canonical decomposition of the sum of two cubes.
b) If x+y = 1 and x^3 +y^3 = 19, find the values of x^2+y^2.
If x+y = 1, then (squaring both sides)
x^2 + 2xy + y^2 = 1. (1)
If x^3 + y^3 = 19, then (x+y)*(x^2 - xy + y^2) = 19 and (replacing here x+y by 1, since it is given)
1*(x^2 - xy + y^2) = 19. (2)
Thus you have these two equations (the system)
(x^2 + y^2) + 2xy = 1 (1)
(x^2 + y^2) - xy = 19. (2)
Subtract eq(2) from eq(1) (both sides). You will get
2xy - (-xy) = 1 - 19, or
3xy = - 18, which implies xy = 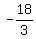 = -6.
Now substitute xy = -6 into eq(1). You will get
x^2 + y^2 = 19 + (-6) = 13.
Answer. x^2 + y^2 = 13.
Doing this way, you do not need solve quadratic equations.
This problem is of the level Math circle = preparation to (local) Math Olympiad = Math+, and the solution I gave you in my post,
is widely considered as a standard solution/approach to such problems.
--------------------
There is another brilliant solution to the same problem. See my lesson
- Advanced lesson on evaluating expressions
in this site, Problem 3.
|
|
|
