|
Question 112136: One number exceeds another by 5. One-fifth of their sum is five less than the smaller number. Find the number.
Found 2 solutions by ptaylor, bucky:
Answer by ptaylor(2198)   (Show Source):
You can put this solution on YOUR website! Let x=smaller number
Then x+5=larger number
Now we are told the following:
1/5(x+x+5)=x-5 multiply each side by 5
x+x+5=5x-25 subtract 5x and also 5 from both sides
x+x+5-5-5x=5x-5x-25-5 collect like terms
-3x=-30 divide both sides by -3
x=10-----------------------smaller number
x+5=10+5=15 ---------larger number
CK
1/5(10+15)=10-5
1/5(25)=10-5
5=5
Hope this helps-----ptaylor
Answer by bucky(2189)  (Show Source):
You can put this solution on YOUR website! The first sentence says that "one number exceeds another ..." This statement tells you that
there are two unknown numbers. Call one of them x and the other y. Since one number
exceeds the other by 5, you know that if you take 5 away from one of the numbers, the result
equals the other number. In equation form this can be written as:
.
 <=== call this your first equation
.
In the next sentence the term "of their sum" tells you that you need to add the two numbers.
Their sum is written as  . Then you need one-fifth of that sum, so you need to
multiply the sum by one-fifth. In algebraic form this is:
.
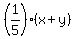 <=== refer to this as the "algebraic form"
.
Finally you are told that this is algebraic form is 5 less than the smaller number.
This means that if you add 5 to this algebraic form the result will equal the smaller
number. From your first equation you can see that y is the smaller of the two numbers
because you have to take 5 away from x to get y. So add 5 to the algebraic
form and the result will equal y. In equation form this is written as:
.
 <=== call this your second equation
.
You now have two independent equations, each with two unknowns. Since there is a match between
the number of equations and the number of unknowns (and the equations are independent
of each other) you can solve for each unknown. Your first equation gives you a value for y
in terms of the second unknown ... which is x. You can see that y is equal to x minus 5.
Therefore, you can go to your second equation and in it you can replace y with x - 5. (This
method is referred to as solving the two equations by "substitution.") When you do this
substitution, the second equation becomes:
.
.
On the left side the quantity (x + (x - 5)) can be simplified. Since the set of parentheses
that contains x - 5 is preceded by a plus sign these parentheses can be removed without
changing the signs of the x and the -5 inside. This leaves you with (x + x - 5) and when
you add the x + x you end up with (2x - 5). Don't forget that this quantity has to be
multiplied by one-fifth, so you now have reduced the left side and the equation is:
.
.
You can now get rid of the  by multiplying both sides of this equation (all terms)
by 5. When you do this multiplication you get:
.
.
This multiplication makes it a little easier because you don't have to mess with fractions.
On the left side combine the two numbers -5 and + 25 to get +20 and the equation then is:
.
.
Let's get rid of the 2x on the left side by subtracting 2x from both sides. When you do
you get:
.
.
Then get rid of the -25 on the right side by adding 25 to both sides to get:
.
.
You can solve for x by dividing both sides by 3 and the result is:
.
.
You now know that x equals 15 and your very first equation told you that if you take 5
away from x the result is y. Therefore, y equals 15 - 5 = 10.
.
So the answer to this problem is x = 15 and y = 10.
.
You can check the answer by returning to the two original equations, substituting
15 for x and 10 for y, and then simplifying to ensure that the left side of the equation
equals the right side.
.
Return to the first equation and when you substitute 15 for x and 10 for y you have:
.
15 - 5 = 10
.
That reduces to:
.
10 = 10
.
so that works.
.
Then go to the second equation and again substitute 15 for x and 10 for y to get:
.
.
Inside the parentheses on the left side the 15 + 10 becomes 25 ... so the equation
reduces to:
.
.
and one-fifth of 25 is 5 so the equation reduces to:
.
.
which simplifies to
.
.
Both your first and second equations work out if x = 15 and y = 10. Therefore, your answers
are correct.
.
Hope this helps you to understand the problem and see how it can be worked out to get
the answer.
.
|
|
|
| |
