Question 1121327: Find the value(s) of the constant k such that the system of linear equations:
9x + ky = 3,
kx + y = 1
has
(i) No solution.
(ii) An infinite number of solutions.
(iii) Exactly one solution.
Found 2 solutions by htmentor, ikleyn:
Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website! (i) No solution.
Parallel lines have the same slope, but not the same y-intercept
Express the equations in standard form:
y = (-9/k)x + 3/k
y = -kx + 1
m1 = -9/k, m2 = -k
m1 = m2 -> -9/k = -k -> k^2 = 9
This gives k = 3, k = -3
k = -3 will result in a different y-intercept
The two equations are
y = 3x - 3
y = 3x + 1
(ii) Using the results from (i), when k = 3, the two equations are the same:
y = -3x + 1
y = -3x + 1
(iii) Any value other than k = 3, k = -3, will result in one intersection point, or one solution
For example, if k = 1 we have
y = -9x + 3
y = -x + 1
Answer by ikleyn(52784)  (Show Source):
You can put this solution on YOUR website! .
If you know what a determinant of a matrix is (if you just learned it), then you can calculate the determinant of the coefficient matrix
det 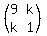 = 9*1 - k*k = 9 - k^2.
The system has no solutions or infinitely many solutions if and only if the determinant is equal to zero
9 - k^2 = 0 ====> k^2 = 9 ====> k = +/- 3.
For all other values of "k", different from 3 or -3, the system has a unique solution.
|
|
|
