Question 1121222: Melanie has 4 different colored crayons and 2 different boxes as shown below. How many different ways can Melanie put all 4 crayons into the 2 boxes so that each box has at least 1 crayon?
Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!
Let's say the four colors are A, B, C, D. Then Box 1 could have, A, B, C, D, AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, or BCD. 14 different ways.
John
My calculator said it, I believe it, that settles it
Answer by ikleyn(52824)  (Show Source):
You can put this solution on YOUR website! .
The question is closely related to this problem:
How many subsets does the set of 4 elements have ?
The answer is 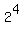 = 16, including empty subset and the improper subset.
So, you can place one subset to one of the two boxes and the rest to the other box.
But the empty subset and the improper subset are excluded by the condition, so only 16-2 = 14 opportunities are available.
Answer. 14.
This way solving the problem becomes especially useful / (effective) when the original set has MANY elements,
so that the direct listing of subsets becomes unpractical.
|
|
|
