.
1. One-equation setup and solution
Let x be the number of dimes (10-cents coins).
Then the number of quarters (25-cents coins) is 30-x.
The "value" equation is
10x + 25(30-x) = 480 cents. (1)
Simplify and solve for x
10x + 750 - 25x = 480
750 - 480 = 25x - 10x
270 = 15x
x = 270/15 = 18.
Answer. 18 dimes and (30-18) = 12 quarters.
Check. 18*10 + 12*25 = 480 cents. ! Correct !
Solved.
2. Two equations setup and solution
x + y = 30 (2) (counting coins)
5x + 25y = 480 (3) (counting cents)
From equation (2), express y = 30-x and then substitute it into equation (4). You will get
5x + 25*(30-x) = 480 (4)
Equation (4) is identical to equation (1) of the 1-st solution.
So, in this way you get the same answer.
Solved.
3. Mental/logic solution without using equations
Assume for a minute that all 30 coins are 10-cents dimes - then the total would be 300 cents, making the shortage of 480-300 = 180 cents.
So, we need to replace some dimes by quarters to compensate the difference.
At each replacement, we diminish the difference by 25-10 = 15 cents, so 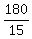 = 12 replacements are required.
Thus, the collection must have 12 quarters, and the rest 30-12 = 18 are dimes.
= 12 replacements are required.
Thus, the collection must have 12 quarters, and the rest 30-12 = 18 are dimes.
Solved (3 times by 3 different methods).
--------------
Congratulations ! You are now familiar with 3 basic methods for solving typical coin problems.
I suggest that algebraic methods will be your basic methods for such problems,
and the logical analysis method will allow you to solve the problems MENTALLY without using equations.
I will be happy if it will make your horizon wider.
--------------
To see other similar solved coin problems, look in the lessons
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Typical coin problems from the archive
- Solving coin problems mentally by grouping without using equations
in this site.
To see how the logical method works for other similar problems, look into the lessons
- Problem on two-wheel and three-wheel bicycles
- Problem on animals at a farm
- Problem on pills in containers
- What type of problems are these?
in this site.