SOLUTION: A grocery stores sells tomatoes in boxes of 4 or 10. If a shopper buys x boxes of 4 and y boxes of 10, where x ≥ 1 and y ≥ 1, for a total of 60 tomatoes, what is one

Algebra ->  Expressions-with-variables -> SOLUTION: A grocery stores sells tomatoes in boxes of 4 or 10. If a shopper buys x boxes of 4 and y boxes of 10, where x ≥ 1 and y ≥ 1, for a total of 60 tomatoes, what is one      Log On


   

Question 1121102: A grocery stores sells tomatoes in boxes of 4 or 10. If a shopper buys x boxes of 4 and y
boxes of 10, where x ≥ 1 and y ≥ 1, for a total of 60 tomatoes, what is one possible value of x?
Found 2 solutions by solver91311, greenestamps:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!








Clearly otherwise

So is bounded above and below by and restricted to the integers (no fractional boxes of 10 tomatoes).

In other words:

Test these values in to eliminate values of that do not result in integer values of


John

My calculator said it, I believe it, that settles it

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


Informally....

The total number of tomatoes is a multiple of 10; and y boxes of 10 each will be a number of tomatoes that is a multiple of 10. Therefore, the total number of tomatoes in the boxes of 4 each must be a multiple of 10.

Multiples of 4 that are multiples of 10, and less than or equal to 60, are 0, 20, 40, and 60.

So the possible numbers of boxes of 4 is 0, 5, 10, or 15.

15 boxes of 4 each would mean 0 boxes of 10 each. Since the problem specifies having at least one box of each size, the possible numbers of boxes of 4 each are 5 and 10.

Answer: the 2 possible values for x are 5 and 10.

The same process, using the formal mathematical method....

4x%2B10y+=+60

Solve for y:

10y+=+60-4x
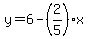
y+=+6+-+%282%2F5%29x

y must be a positive integer; and 6 is an integer. That means(2/5)x must be an integer; and that means x must be a multiple of 5.

The conditions of the problem say x must be a positive integer, and that the value of x must be less than 15. Since we have determined that it also must be a multiple of 5, the only 2 possible values of x are 5 and 10.