Question 1121074: Two Coast Guard stations, A and B, are on an east-west line and are 110 km apart. The bearing of a ship from station A is S 56o E, and the bearing of the same ship from station B is S 38o W.
a) How far is the ship from the east-west line connecting the two Coast Guard stations.
b) How far is the ship from station A?
c) How far is the ship from station B?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can draw triangle ABC as shown in the diagram below:
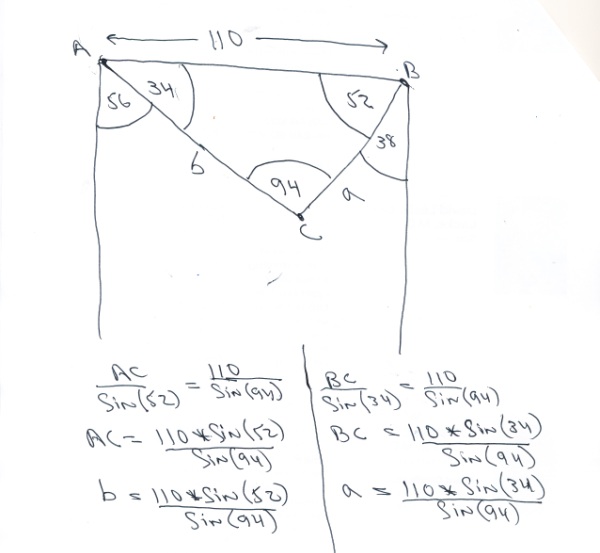
line segment AB of this triangle is equal to a distance of 110 kilometers.
point A of this triangle is one of the stations.
point B of this triangle is the other one of the stations.
point C of this triangle is the location of the ship.
the ship is 56 degrees south east of point A and 38 degrees south west of point B, as shown in the diagram.
line segment AB in the diagram is a horizontal line because it is on the east-west line of the diagram.
the vertical lines emnating from point A and B form a 90 degree with the horizontal line.
angle A of triangle ABC is therefore equal to 90 - 56 = 34 degrees.
angle B of triangle ABC is therefore equal to 90 - 38 = 52 degrees.
since the sum of the angles of a triangle is 180 degrees, that makes angle C equal to 94 degrees.
110 kilometers is opposite angle C of this triangle.
line segment b is opposite angle B of this triangle.
line segment a is opposite angle A of this triangle.
by the law of sines, 110 / sin(C) = a / sin(A) = b / sin(B)
to find a, you would take 110 / sin(C) = a / sin(A)
to find b, you would take 110 / sin(C) = b / sin(B)
solve for a to get a = 110 * sin(A) / sin(C)
solve for b to get b = 110 * sin(B) / sin(C)
these equations become:
a = 110 * sin(34) / sin(94) = 61.66142351 kilometers.
b = 110 * ain(52) / ain(94) = 86.89284951 kilometers.
b is the distance of the ship from location A.
a is the distance of the ship from location B.
a is equal to line segment BC in the diagram.
b is equal to line segment AC in the diagram.
note that a = 110 * sin(34) / sin(94) is the same as BC = 110 * sin(34) / sin(94) as shown in the diagram.
in other words, a and line segment BC are one and the same line segment.
note also that b = 110 * ain(52) / ain(94) is the same as AC = 110 * sin(52) / sin(94) as shown in the diagram.
in other words, b and line segment AC are one and the same line segment.
your solution is that the distance of the ship from point A is 86.89284951 kilometers and the distance of the ship from point B is 61.66142351 kilometers.
|
|
|