.
First step of the solution is to transform the inequality to the STANDARD FORM having the rational function in the left side
presented with the numerator and denominator decomposed as the products of linear factors and having 0 (zero) at the right side.
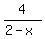 <=
<= 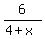
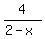 -
- 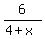 <= 0
<= 0
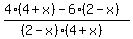 <= 0
<= 0
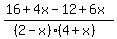 <= 0
<= 0
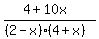 <= 0
<= 0
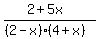 <= 0
<= 0
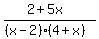 >= 0 (1)
Notice that in the last line I replaced (2-x) in the denominator with (x-2) and changed the inequality sigh to the opposite one.
Now all the terms in the rational function are of the form (x-c), where "c" is the constant, so they are easy to analyse.
>= 0 (1)
Notice that in the last line I replaced (2-x) in the denominator with (x-2) and changed the inequality sigh to the opposite one.
Now all the terms in the rational function are of the form (x-c), where "c" is the constant, so they are easy to analyse.
First step is done.
From this point, the standard analysis begins, and it completes the solution.
There are 3 critical points, x= -4, x= -2/5 and x= 2. The domain is the number line except x= -4 and x= 2.
The critical points divide the number line in 4 intervals:
1) ( ,
, ) 2) (
) 2) ( ,
,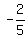 ] 3) [
] 3) [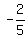 ,
, ) and 4) (
) and 4) ( ,
, ).
a) in the first interval, all three binomials of (1) are negative; hence, the rational function (1) is negative.
Thus this interval (
).
a) in the first interval, all three binomials of (1) are negative; hence, the rational function (1) is negative.
Thus this interval ( ,
, ) is NOT the solution.
b) in the second interval, one of the three binomials of (1) is positive, while the other two are negative.
Hence, the rational function (1) is positive.
Thus this interval (
) is NOT the solution.
b) in the second interval, one of the three binomials of (1) is positive, while the other two are negative.
Hence, the rational function (1) is positive.
Thus this interval ( ,
,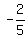 ] IS the solution.
c) in the third interval, two of the three binomials of (1) are positive, while the single one is negative.
Hence, the rational function (1) is negative.
Thus this interval [
] IS the solution.
c) in the third interval, two of the three binomials of (1) are positive, while the single one is negative.
Hence, the rational function (1) is negative.
Thus this interval [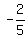 ,
, ) is NOT the solution.
d) Finally, in the fourth interval, all three binomials of (1) are positive.
Hence, the rational function (1) is positive.
Thus this interval (
) is NOT the solution.
d) Finally, in the fourth interval, all three binomials of (1) are positive.
Hence, the rational function (1) is positive.
Thus this interval ( ,
, ) IS the solution.
Answer. The solution is the set (
) IS the solution.
Answer. The solution is the set ( ,
,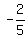 ] U (
] U ( ,
, ).
).
To see many other similar solved problems, look into the lesson
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
in this site.