.
From this functional equation
f(a+b) = f(a) + f(b)
you have
f(0) = f(0) + f(0) ====> f(0) = 2*f(0) ====> f(0) = 0,
and also
f(2) = 2*f(1), f(3) = 3*f(1), f(4) = 4*f(1), . . . . , f(2008) = 2008*f(1).
Since f(2008) = 3012 by the condition, it implies that 2008*f(1) = 3012, and, hence, f(1) = 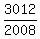 =
=  .
Then f(2009) = 2009*f(1) =
.
Then f(2009) = 2009*f(1) =  .
Answer. f(2009) =
.
Answer. f(2009) =  =
=  .
.