Question 1120785: Hi there!
I'm having a tough time trying to figure out how to solve the following rational inequality.
(x+2)/(x-4)<3
All of my teachers examples have big charts and graphs at the bottom of each solution (an interval chart I believe?) And I really do not understand the chart.
Anyways if anyone knows what this chart is and how I would go about solving the equation like that you would be a total life saver! Thanks so much in advance.
Found 2 solutions by greenestamps, solver91311:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
There are many variations of how to present the method for solving inequalities like this; I can't be sure what your teacher does. I will explain one common method and hope it is something like what you have seen.
The first thing to do is get everything on one side of the inequality. This is because by far the easiest way to solve an inequality like this is to have one side equal to 0. So
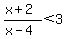
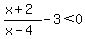
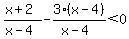 (Get a common denominator)
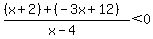
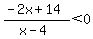
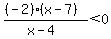
The left side of the inequality now has three factors in the numerator or denominator: (-2), (x-7), and (x-4). The left side, because of the factor x-7 in the numerator, is equal to 0 when x=7; because of the factor of (x-4) in the denominator, it is undefined when x=4.
So the values of x=4 and x=7 are the values for which one of the factors on the left is equal to 0. That means those two values divide the number line (of x values) into three parts: x less than 4; x between 4 and 7, and x greater than 7.
The inequality is solved by looking at values in each of those intervals to determine in which interval(s) the expression on the left is negative, as required.
(1) For x less than 4, (-2) is negative, (x-4) is negative, and (x-7) is negative. Three negative factors in the expression make the expression value negative; so x<4 is part of the solution set of the inequality.
(2) For x between 4 and 7, (-2) is negative, (x-4) is positive, and (x-7) is negative. Two negative factors make the expression value positive; so the interval between 4 and 7 is NOT part of the solution set.
(3) For x greater than 7,(-2) is negative and both (x-4) and (x-7) are positive. That makes the expression value negative; so the interval x>7 is part of the solution set.
So the inequality is true for x less than 4, and for x greater than 7. Finally, noting that the expression is 0 for x=7 and undefined for x=4, the solution set (in standard interval notation) is (-infinity,-4) union [7,infinity).
Answer by solver91311(24713)  (Show Source):
|
|
|
.
