SOLUTION: For what values of m is the line y= mx a tangent to the parabola y=x^2 - 8x + 25?

1.  The equation for the common point of the straight line  y = mx  and the parabola  y = x^2 - 8x + 25  is


    mx = x^2 - 8x + 25,    or


    x^2 - (8+m)*x + 25 = 0.        (1)



2.  The straight line is the tangent to the parabola if the two roots of the equation (1) merge into one root.


    The necessary and sufficient condition for it is equality of the discriminant of the equation (1) to zero:


    d = b^2 - 4ac = 0,


        where  a= 1, b = -(8+m)  and  c= 25:


    d = 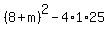 = 0,    or


    64 + 16m + m^2 - 100 = 0,

    m^2 + 16m - 36 = 0,

    (m-2)*(m+18) = 0.


This equation has two solutions:  m= 2  and  m= -18.


Answer.  The problem has two solutions:  m= 2  and  m= -18.