SOLUTION: Given regular hexagon ABCDEF,, with Centre O and sides of length 12. Let G be the midpoint of BC. Let H be the midpoint of DE. AH intersects EB at J and FG intersects EB at K..F

Algebra ->  Triangles -> SOLUTION: Given regular hexagon ABCDEF,, with Centre O and sides of length 12. Let G be the midpoint of BC. Let H be the midpoint of DE. AH intersects EB at J and FG intersects EB at K..F      Log On


   

Question 1120495: Given regular hexagon ABCDEF,, with Centre O and sides of length 12. Let G be the midpoint of BC. Let H be the midpoint of DE. AH intersects EB at J and FG intersects EB at K..Find JK.
Hint given in question ::: draw auxiliary lines HG and DA.
Thanks for any help .
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


I didn't see any use in the suggested auxiliary line segments HG and DA....

Perhaps there is a clever way to solve the problem using them; my solution is not very difficult.

Consider the regular hexagon with the center O at (0,0), with sides AB and DE horizontal; A in quadrant III, B in quadrant IV, D in quadrant I, and E in quadrant II. Then the coordinates of the vertices of the hexagon are

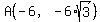
A%28-6%2C-6%2Asqrt%283%29%29
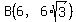
B%286%2C6%2Asqrt%283%29%29
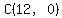
C%2812%2C0%29
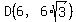
D%286%2C6%2Asqrt%283%29%29
E%28-6%2C6%2Asqrt%283%29%29
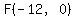
F%28-12%2C0%29

Then the two midpoints in the problem have coordinates

G%289%2C-3%2Asqrt%283%29%29
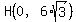
H%280%2C6%2Asqrt%283%29%29

Now triangles HJE and AJB are similar, with the ratio of similarity 1:2 because of the lengths of the bases EH (length 6) and AB (length 12). Since the height of the hexagon is 12*sqrt(3), we can determine that the y coordinate of point J is 2*sqrt(3). (It is 1/3 of the way from side DE -- y value 6*sqrt(3) -- and side AB -- y value -6*sqrt(3).)

So we can determine that the coordinates of J are 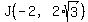J%28-2%2C2%2Asqrt%283%29%29.

The exact same similarity exists between triangles BKG and EKF, leading us to the coordinates of K as 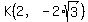K%282%2C-2%2Asqrt%283%29%29.

Then, making JK the hypotenuse of a right triangle, the Pythagorean Theorem (or the observation that we have a 30-60-90 right triangle, with legs 4 and 4*sqrt(3)) gives us the length of JK as 8.