Question 1120480: Jimmy opens a savings account with a $280 deposit at the beginning of the month. The account earns 4.3% annual interest compounded monthly. At the beginning of each subsequent month, Jimmy deposits an additional $280. How much will the account be worth at the end of 14 years? $
Found 3 solutions by ankor@dixie-net.com, MathTherapy, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Jimmy opens a savings account with a $280 deposit at the beginning of the month.
The account earns 4.3% annual interest compounded monthly.
At the beginning of each subsequent month, Jimmy deposits an additional $280.
How much will the account be worth at the end of 14 years? $
:
14 * 12 = 168 periods
:
The annuity formula:
FV = 280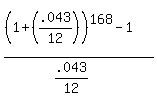
do the math
FV = 280(229.8985)
FV = $64,371.60
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Jimmy opens a savings account with a $280 deposit at the beginning of the month. The account earns 4.3% annual interest compounded monthly. At the beginning of each subsequent month, Jimmy deposits an additional $280. How much will the account be worth at the end of 14 years? $
You need to apply the formula for future value of an ANNUITY DUE, or:  , and
NOT the one for future value of an ORDINARY ANNUITY. This should yield:  , as opposed to $64,371.60.
This is the difference between making payments, or depositing at the BEGINNING of a period, instead of at the end of the period.
For the above:
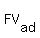 is: FUTURE VALUE of an ANNUITY DUE (Unknown, in this case)
PMT is: PERIODIC PAYMENT made ($280, in this case)
"i" is: ANNUAL Interest rate (4.3%, or .043, in this case)
m is: number of ANNUAL COMPOUNDING periods (12, in this case)
t is: Time, in years it takes to reach Future Value (14 years, in this case)
Answer by ikleyn(52781)  (Show Source):
|
|
|
