Question 1120393: Can there exist a triangle ROS in which the trisectors of angle O intersect RS at D and E with RD =1,,DE=2,andES=4? Explain
Thanks for any help .
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Make a sketch. I will refer to it as if you have it in front of you (as I have it in front of my eyes).
+---------------------------------------------------------------+
| Let ROS be a triangle, and let its angle ROS at vertex O |
| is trisected in a way that RD= 1, DE=2 and ES=4. | (*)
+---------------------------------------------------------------+
I am going to bring it to contradiction and prove, in this way, that such trisection IS NOT POSSIBLE.
Let "t" be any of the three congruent small angles at vertex O.
Let "a" be the length of RO; let "b" be the length of DO.
Then the length of EO is 2a (bisector theorem for triangle REO),
and the length of SO is 2b (bisector theorem for triangle DOS).
I will remind you, that the bisector theorem STATES that
the ratio of the segments lengths, to which the bisector of a triangle
divides the opposite side is equal to the ratio of the lengths
of the two lateral corresponding sides.
Now, triangle ROD has side lengths "a" and "b", that conclude the angle "t", and the opposite side RD= 1.
So, we write the Cosine Law formula for RD
RD^2 = 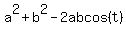 = 1^2. (1)
Next, triangle DOE has side lengths "b" and "2a", that conclude the angle "t", and the opposite side DE= 2.
So, we write the Cosine Law formula for DE
DE^2 = = 1^2. (1)
Next, triangle DOE has side lengths "b" and "2a", that conclude the angle "t", and the opposite side DE= 2.
So, we write the Cosine Law formula for DE
DE^2 = 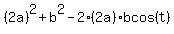 = 2^2. (2)
Finally, triangle EOS has side lengths "2a" and "2b", that conclude the angle "t", and the opposite side ES= 4.
So, we write the Cosine Law formula for ES
ES^2 = = 2^2. (2)
Finally, triangle EOS has side lengths "2a" and "2b", that conclude the angle "t", and the opposite side ES= 4.
So, we write the Cosine Law formula for ES
ES^2 = 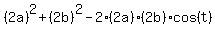 = 4^2. (3)
I will rewrite the three equations (1), (2) (3) in simpler form = 4^2. (3)
I will rewrite the three equations (1), (2) (3) in simpler form
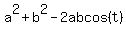 = 1. (1') = 1. (1')
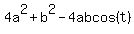 = 4. (2') = 4. (2')
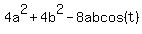 = 16. (3')
Now compare equations (1') and (3'). You see that the left side of (3') is four times the left side of (1'),
but the right side of (3') is sixteen times left side of (1').
It is the contradiction, and this contradiction proves that the original assumption (*) is not valid / (is not possible). = 16. (3')
Now compare equations (1') and (3'). You see that the left side of (3') is four times the left side of (1'),
but the right side of (3') is sixteen times left side of (1').
It is the contradiction, and this contradiction proves that the original assumption (*) is not valid / (is not possible).
At this point, my proof is completed.
//////////////
It is also possible to construct another proof, using the similarity properties of small triangles.
Indeed, from one hand side, triangles ROD and EOS must be similar with the similarity coefficient of 2,
because their "lateral" sides are proportional RO : DO = a : b = EO : SO = (2a) : (2b) and the concluded angles "t" are congruent;
but from the other hand side, their sides, opposite to angle "t", are with the ratio 4:1, which gives the CONTRADICTION.
|
|
|