SOLUTION: Solve the following inequalities by stating the solution set or on a number line. Show your work. (x+5)(x-3)≥-x^2+7x-3

Algebra ->  Systems-of-equations -> SOLUTION: Solve the following inequalities by stating the solution set or on a number line. Show your work. (x+5)(x-3)≥-x^2+7x-3      Log On


   

Question 1120250: Solve the following inequalities by stating the solution set or on a number line. Show your work. (x+5)(x-3)≥-x^2+7x-3
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
This is x^2+2x-15>=x^2+7x-3
-5x >=+12
x < = -2.4
Check by trying 0 which should not work
-15 >=-3 does not work'
and -3 which should work
-12 >=-13 which is true.
graph%28300%2C300%2C-10%2C10%2C-20%2C10%2Cx%5E2%2B2x-15%2Cx%5E2%2B7x-3%29

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Solve the following inequalities by stating the solution set or on a number line. Show your work. (x+5)(x-3) >= -x^2+7x-3
~~~~~~~~~~~~~~~~~ 

(x+5)(x-3) >= -x^2+7x-3  ====>

x^2 + 5x - 3x - 15 >= -x^2 + 7x - 3  ====>  subtract  (-x^2+7x-3)  from both sides  ====>  

2x^2 - 5x - 12 >= 0

x^2 - 2.5x - 6 >= 0  ====>  factor left side  ====>

(x+1.5)*(x-4) >= 0


The solution is the union of two semi-infinite intervals  -infinity < x <= -1.5 U 4 <= x < infinity.


Or, in the interval notation,  (-infinity,-1.5] U  [4,infinity).


          VISUAL CHECK






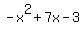Plot y = (x+5)(x-3) (red)  and y = -x%5E2%2B7x-3.


The solution set are those points "x" in x-axis, where the red line is above the green line.

Solved.