|
Question 1120141: Ten balls numbered 1 to 10 are in a jar. Jack reaches into the jar and randomly removes one of the balls. Then Jill reaches into the jar and randomly removes a different ball. What is the probability that the sum of the two numbers on the balls removed is even?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website! .
Let me reformulate the problem in more precise / (more correct) form:
Ten balls numbered 1 to 10 are in a jar. Jack reaches into the jar and randomly removes two of the balls.
What is the probability that the sum of the two numbers on the balls removed is even?
This phrase "Then Jill reaches into the jar and randomly removes a different ball." of the original condition is not necessary . . .
He FOR SURE will remove a different ball, since he does not replace the first one . . .
Solution
The number of all combinations of pairs of the balls is  =  = 45.
The favorable events happen when both the balls in a pair are even, OR when both the balls in a pair are odd.
The even numbers from 1 to 10 are 2, 4, 6, 8 and 10.
The number of combinations where both balls are even is 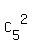 =  = 10.
The odd numbers from 1 to 9 are 1, 3, 5, 7, and 9.
The number of combinations where both balls are odd is 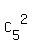= = 10.
Thus of 45 possible outcomes, only 10 + 10 = 20 are favorable.
Hence, the probability under the question is  =  .
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The wording of the problem implies the ball Jack selects is not replaced before Jill selects a ball.
The sum is even if both balls selected are even, or if both are odd.
P(even, even) = (5/10)(4/9) = 20/90 = 2/9
P(odd, odd) = (5/10)(4/9) = 20/90 = 2/9
The probability that the sum is even is 2/9+2/9 = 4/9.
Note we can easily confirm this answer by verifying that the probability of an odd sum is 5/9. This also gives us practice in performing these kinds of probability calculations.
The sum is odd if the first is even and the second is odd, or vice versa.
P(even, odd) = (5/10)(5/9) = 25/90
P(odd, even) = (5/10)(5/9) = 25/90
P(odd sum) = 25/90+25/90 = 50/90 = 5/9
The calculations above were made in such a way that we are considering Jack selecting a ball and then Jill selecting a ball as consecutive events.
We can also calculate probabilities of this kind viewing the problem as having the two of them select the balls at the same time. Being able to solve the problem by this method is useful, because in more complicated problems one or the other of the methods might be far easier than the other.
Together they are selecting 2 of the 10 balls; the number of ways they can do that is "10 choose 2":
C(10,2) = (10*9)/2 = 45.
To get an even sum they have to choose either 2 of the 5 even balls and 0 of the 5 odd balls, or 2 of the 5 odd balls and 0 of the even balls:
C(5,2)*C(5,0)+C(5,2)*C(5,0) = 10*1+10*1 = 20.
To get an odd sum they have to choose 1 of the 5 even balls and one of the 5 odd balls:
C(5,1)*C(5,1) = 5*5 = 25.
Then the probability of getting an even sum is 20/45 = 4/9; the probability of getting an odd sum is 25/45 = 5/9.
|
|
|
| |
