Question 1120095: A hemispherical bowl of diameter 14cm mounted on a bucket in the form of a frustum of a cone. If the base diameter of the bucket is 7cm and the total height of the figure is 21cm, calculate the total surface area of the figure. (Take pie = 22/7)
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From your description, I have a picture that is in the shape of a bird bath.
But I can't see how the problem can be answered without knowing the diameter or radius of the top base of the frustum.
And even if we have that information, finding the total surface area will be difficult at best, because part of the surface of the hemispherical bowl will be covered by the frustum.
To have any chance of getting an answer, the problem needs to be more clearly and completely defined.
-------------------------------------------------------------------
Revised description:
A hemispherical bowl of diameter 14cm mounted on a bucket in the form of a frustum of a cone. If the top and base diameter of the bucket are 14cm and 7cm respectively and the total height of the figure is 21cm, calculate the total surface area of the figure. (Take pie = 22/7). The figure is combined that the hemispherical bowl and the bucket are together.
That makes the problem workable; the top face of the frustum and the flat surface of the hemisphere are both circles with diameter 14cm.
The total surface area of the figure is then (1) the curved surface of the hemisphere; (2) the flat surface of the bottom base of the frustum; and (3) the lateral surface of the frustum of the cone.
(1) The surface area of a sphere is 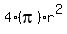 . The diameter is 14cm, so the radius is 7cm; the curved surface area of the hemisphere is . The diameter is 14cm, so the radius is 7cm; the curved surface area of the hemisphere is  . .
(2) The bottom base of the bucket (frustum of a cone) is a circle with diameter 7cm so radius 3.5cm; its area is  . .
(3) The lateral surface area of a cone is 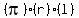 where l is the slant height. where l is the slant height.
Consider the frustum as a full cone with a smaller cone cut off. Since the height of the whole figure is 21cm and the radius of the hemisphere is 7cm, the height of the frustum is 14cm. Then, since the diameter of the top base of the frustum is twice the diameter of the bottom base (14cm and 7cm), the height of the "full" cone is twice the height of the frustum, or two times 14cm, or 28cm.
Then the slant height of the full cone (from the Pythagorean Theorem) is  . .
The lateral surface area of the "full" cone is then  . .
Finally, the height of the cone that was cut off to make the frustum is half the height of the full cone. Then, since the original "full" cone and the smaller cone that was cut off are similar, the lateral surface area of the small cone that was cut off is one-fourth (one half, squared) of the lateral surface area of the whole cone. So the lateral surface area of the frustum is  . .
And so the total surface area of the figure is then
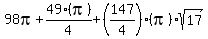
|
|
|