SOLUTION: Joey has 24 coins in his pocket. The coins are all nickels and dimes. The total value of the coins is $1.85. How many dimes does Joey have?

     = 13 dimes.


    The rest 24 - 13 = 11 are nickels.


    Check.  11*5 + 13*10 = 185 cents.   ! Correct !


    Answer.  13 dimes, 11 nickels.

Let assume that all 24 coins are nickels.  Then their total value would be 5*24 = 120 cents.


But the real value is 185, and the difference is  1805- 120 = 65 cents.   

    Notice, this difference is the NUMERATOR in my one-line solution.


Surely, you understand that the cause of this difference lies in the fact that we counted some dimes as nickels.


Now let's replace nickels by dimes. At each replacement, we decrease the difference in 5 cents,

so the total number of replacements is  the rat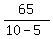io   = 5 cents.


     Notice, this difference  10-5 = 5 cents is the DENOMINATOR  in my one-line solution.


Thus the ratio   =  = 13  is exactly the number of dimes in the collection.


This completes the explanation.