Question 1119882: Need help please.
I'm trying to figure out how to find three ordered pairs that satisfy the equation 4 + 2y = 3x.
I've been staring at this for a while, read, and researched, but cannot figure it out.
More than anything, I would like to understand how to get the intercepts, not just an answer.
Thank you!
Found 2 solutions by math_helper, MathTherapy:
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! There are more than 3 ordered pairs. In fact, there are an infinite number of ordered pairs that satisfy the equation. I will show you how to find some, at will.
First, solve the equation for y:
2y = 3x - 4
y = (3/2)x - 2
Pick a value for x, plug it in on the right hand side and calculate, that's y. The ordered pair (x,y) is an satisfies the equation.
————————
Examples:
x=0 —> y = (3/2)(0) - 2 = -2 —> (0,-2) is an ordered pair that satisfies the equation
x=1 —> y = (3/2)(1) - 2 = -1/2 —> (1, -1/2) is another
x=2 —> y = (3/2)(2) - 2 = 1 —> (2, 1) is a third
You can pick any value of x that you want:
x=-10 —> y = (3/2)(-10) - 2 = -17 —> (-10, -17) is a fourth
etc.
Answer by MathTherapy(10556)  (Show Source):
You can put this solution on YOUR website! Need help please.
I'm trying to figure out how to find three ordered pairs that satisfy the equation 4 + 2y = 3x.
I've been staring at this for a while, read, and researched, but cannot figure it out.
More than anything, I would like to understand how to get the intercepts, not just an answer.
Thank you!
4 + 2y = 3x
2y = 3x - 4 ----- Subtracting 4 from each side
 ------ Dividing by 2
Now, since the DENOMINATOR of the coefficient on x is 2, then the easiest and best values to substitute for x would be EVEN NUMBERS,
and better yet, 0 and other SMALL POSITIVE EVEN numbers, the likes of: 2, 4, and 6. This will give you 4 coordinates:
1) 
This results in coordinate point: (0, - 2). This is also the y-intercept as x = 0.
2) 
This results in coordinate point: (2, 1).
3) 
This results in coordinate point: (4, 4).
4) 
This results in coordinate point: (6, 7).
For the y-intercept, simply substitute 0 for x to find it. This was done above.
For the x-intercept, simply substitute 0 for y to find it, as follows:
4 + 2y = 3x
4 + 2(0) = 3x
4 = 3x
This results in coordinate point:  .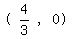
|
|
|
