Question 1119820: Help please.
I don’t think I’m doing it right.
Write the slope-intercept form of the equation of the line through the given points.
(5, -5) and (-3, 4)
Am I supposed to find the slope first? m=y2-y1/x2-x1?
If so, what do you do after that.
I found 2 different slopes: 9 -9
- — & —
2 8
Any help is appreciated!
Found 5 solutions by josgarithmetic, Alan3354, MathTherapy, ikleyn, greenestamps:
Answer by josgarithmetic(39621)   (Show Source):
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! Write the slope-intercept form of the equation of the line through the given points.
(5, -5) and (-3, 4)
Am I supposed to find the slope first? m=y2-y1/x2-x1?
If so, what do you do after that.
I found 2 different slopes: 9 -9
- — & —
2 8
====================
There's only 1 slope per line.
(x1,y1) and (x2,y2) have to match.
m = (-5-4)/(5 - (-3)) = -9/8
-------
Then:
y - y1 = m*(x-x1) where (x1,y1) is either point.
y+5 = (-9/8)*(x-5) = -9x/8 = 45/8
Slope-intercept form means solve for y
Or 
Answer by MathTherapy(10555)  (Show Source):
Answer by ikleyn(52824)  (Show Source):
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
It's easy to see how you can get two different values for the slope; but of course there can only be one right value.
I see many students getting wrong values for the slope by blindly plugging numbers into the slope formula,  .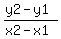
For any students who find themselves getting wrong values for the slope using the formula, I recommend visualizing the two points on a graph and calculating slope using the "rise over run" concept.
You are far less likely to get wrong numbers if you do that, instead of blindly plugging numbers into a formula.
I always like to start at the leftmost point so that my "run" is positive. Then the slope will tell me how much I move up (positive slope) or down (negative slope) for each "step" I take forward.
In this problem, the point (-3,4) is to the left of (5,-5). The run (from -3 to 5) is 8; in moving from x=-3 to x=5 my y value changes from 4 to -5, a change of -9. So the slope is my "rise over run", which is -9/8.
Note that if you have a picture at least in your mind of the two points, you are less likely to make mistakes in calculating the slope.
For example, you say you got two values for the slope, one of which was -9/2. It is easy to see how you can get the "2" in the denominator if you blindly plug numbers into the slope formula, when the x coordinates of the two points are 5 and -3. But if you have a picture of the two points in your mind (or on paper), it is easy to see that the difference between the two x values is 8 and not 2.
Then once you have the correct slope of -9/8, proceed to find the equation using either either the point-slope form or the slope-intercept form of a linear equation.
|
|
|
