SOLUTION: Flying with the wind, a plane traveled 420 miles in 3 hours. Flying against the wind, the plane traveled the same distance in 5 hours. Find the rate of the plane in calm air and th

Let u = rate of the plane in calm air, in miles per hour;

    v = rate of wind.


Then the effective speed flying with 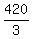the wind is   = 140 mph.

It is the sum u + v, so your first equation is

u + v = 140.    (1)



The effective speed flying against the wind is 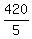  = 84 mph.

It is the difference u - v, so your second equation is

u - v =  84.    (2)


Thus you have the system of two linear equations (1) and (2).

To solve it, add the equations.  You will get


2u = 140 + 84 = 224  ====>  u = 224/2 = 112.


Then from equation (1)  v = 140 - 112 = 28.


Answer.  The rate of the plane in calm air is  112 miles per hour.

         The rate of the wind is 28 miles per hour.


Check.   Check the solution on your own.

         After doing it, you will understand the solution much better.