.
Answer. The smallest positive integer that has exactly 6 divisors is 12 =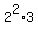 
.
Solution.
1. For integer number N =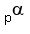 
, where p is a prime number and 
is an integer exponent (index),
the number of divisors is 
.
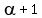You can easily check it: the divisors are 1, p, 
, . . . , .
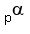2. For integer number N =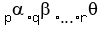 
, where p, q, . . . , r are prime divisors and , 
, . . . , 
are integer exponents (indexes)
the number of divisors is 
.
3. From these facts, you can easily obtain the answer.
Notice that 6 = 2*3.
It is easy to list those divisors: 1, 2, 4, 3, 6, 12.
