SOLUTION: Three numbers are in the ratio of 1:5:9. If the second number is diminished by 8, the three numbers will form a geometric sequence. What are the three numbers?

Click here to see ALL problems on Sequences-and-series

Question 1119640: Three numbers are in the ratio of 1:5:9. If the second number is diminished by 8, the three numbers will form a geometric sequence. What are the three numbers?
Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

Since obtaining the geometric sequence did not involve altering the first and third terms, the third term must be times the first. From this, we conclude that the common ratio is 3.

Since the given numbers are in the ratio 1:5:9, they can be expressed as:

From our analysis of the common ratio, we know that the geometric sequence must be:

And we know that must be 8 larger than and that . From this we have:

so the geometric sequence must be

And then the original three numbers must be:

John

My calculator said it, I believe it, that settles it

Answer by ikleyn(52790) (Show Source):
You can put this solution on YOUR website!
.
The problem has 2 (two) solutions/answers.

One answer (as found by John) for three numbers is 4, 20, 36.

The other answer for three numbers is 1, 5, 9.

Solution

From the condition, the three numbers are x, 5x and 9x. The condition that three numbers x, (5x-8) and 9x form a geometric progression is this equality (equation) 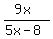= 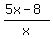, (1) saying that the ratio of the third to the second term of the GP is the same as the ratio of the second to the first. From (1), 9x^2 = (5x-8)^2, 9x^2 = 25x^2 - 80x + 64, 16x^2 - 80x + 64 = 0 with the roots = 4, = 1.

Solved.