|
Question 1119540: Find the smallest possible value:
 + +  + + 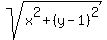 + + 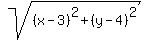
If you can, answer in root and numeral form, please.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The key to the solution of the problem is to recognize that the given expression is the sum of distances from the point (x,y)
in a coordinate plane to the points (0,0), (0,1), (1,0) and (3,4).
Theorem
For a convex quadrilateral in a plane, the point in the plane which minimizes the sum of the distances from the point to vertices
of the quadrilateral is the intersection of its diagonals.
Similar statement for a triangle leads to Fermat's point of a triangle and is considered as a difficult geometry
conception and statement, which goes far beyond and above the elementary geometry level.
See this Wikipedia article https://en.wikipedia.org/wiki/Fermat_point .
But for a quadrilateral it is ELEMENTARY statement accesible and approachable for starters.
Proof
Let ABCD be the given quadrilatersl in a plane with the verices A, B, C and D (in this order).
Let "O" be the intersection point of its diagonals AC and BD.
And let X be any other point in the plane.
The sum of distances from X to vertices is
d(X) = |AX| + |BX| + |CX| + |DX|.
The sum of distances from O to vertices is
d(O) = |AO| + |BO| + |CO| + |DO|.
By applying the "triangle inequality", you have
d(O) = (|AO| + |CO|) + (|BO| + |DO|) = |AC| + |BD| < (|AX| + |CX|) + (|BX| + |DX|) = d(X),
and the statement is PROVED.
Therefore, the solution to your problem is THIS:
The point in the plane which gives the minimum to your expression is the intersection point of the segment
connecting the points A=(0,0) and C=(3,4) with the segment connecting the points B=(0,1) and D=(1,0).
The straight line connecting the points A and C is
y = 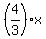 . (1)
The straight line connecting the points B and D is
y - 1 = -x. (2)
Their intersection is the point . (1)
The straight line connecting the points B and D is
y - 1 = -x. (2)
Their intersection is the point
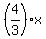 = 1 - x ====> 4x = 3 - 3x ====> 7x = 3 ====> x = = 1 - x ====> 4x = 3 - 3x ====> 7x = 3 ====> x = 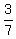 ; y = ; y = 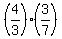 = =  .
To find the minimum of the given expression, you need to find the lengths of the diagonals |AC| and |BD| and add them.
|AC| = .
To find the minimum of the given expression, you need to find the lengths of the diagonals |AC| and |BD| and add them.
|AC| =  = =  = =  = 5;
|BD| = = 5;
|BD| =  .
So, the minimum of the given expression is .
So, the minimum of the given expression is  .
Answer. The point which gives the minimum to the given expression is (x,y) = ( .
Answer. The point which gives the minimum to the given expression is (x,y) = (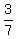 , , ).
The value of the minimum is ).
The value of the minimum is  . .
******************
* * * SOLVED * * *
******************
|
|
|
| |