Question 1119463: find three consecutive integers such that the product of the first two plus the product of the last two is 8
Found 3 solutions by math_helper, ankor@dixie-net.com, MathTherapy:
Answer by math_helper(2461)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! find three consecutive integers
a, a+1, a+2
such that the product of the first two plus the product of the last two is 8
a*(a+1) + (a+1)(a+2) = 8
a^2 + a + a^2 + 2a + 1 + 2 = 8
2a^2 + 3a + 3 - 8 = 0
2a^2 + 3a - 5 = 0
Factors to
(2a+5)(a-1) = 0
only one integer solution
a = 1
:
the integers 1, 2, 3
:
:
check
(1*2) + (2*3) = 8
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! find three consecutive integers such that the product of the first two plus the product of the last two is 8
One of the easiest methods to solve this is to first let the 2nd integer be S
Then 1st = S - 1, and 3rd: S + 1
From what was given, we can say that: (S - 1)S + S(S + 1) = 8
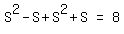
 =====> =====> 
Therefore, 2nd integer, or 
If the 2nd = 2, then the 1st and 3rd = S - 1, or 2 - 1, or 1, and S + 1, or 2 + 1, or 3. Integers are therefore: 
If the 2nd = - 2, then the 1st and 3rd = S - 1, or - 2 - 1, or - 3, and S + 1, or - 2 + 1, or - 1. Integers are therefore: 
You're most welcome, @math_helper. Was more than happy to share!
|
|
|