Question 1119315: If Drink A contains 1% sugar and Drink B contains 79% sugar. How much of each solution should be mixed in order to create 120 milliliters of a solution that contains 66% sugar?
Found 4 solutions by Alan3354, solver91311, ikleyn, greenestamps:
Answer by Alan3354(69443)   (Show Source):
Answer by solver91311(24713)  (Show Source):
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
Let x be the amount of the drink B to mix, im milliliters.
Then the amount of the drink A must be (120-x) milliliters.
The sugar content equation is this
0.01*(120-x) + 0.79x = 0.66*120
Simplify and solve for x:
1.2 - 0.01x + 0.79x = 0.66*120
0.78x = 0.66*120 - 1.2 = 78.
x = 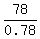 = 100.
Answer. 100 mL of the drink B and (120-100) = 20 mL of the drink A.
Check. 0.79*100 + 0.01*20 = 79.2 grams of sugar.
0.66*120 = 79.2 grams of sugar. ! Correct !
-----------------
It is a standard and typical mixture problem.
For introductory lessons covering various types of mixture word problems see
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is an alternative to the traditional algebraic solution method shown by the other tutors. If you understand how to use it, you will get your answer to problems like this much faster and with far less effort.
The key idea is that the ratio in which the two ingredients are mixed exactly determines where the percentage of the mixture lies between the percentages of the two ingredients.
To see how easy this method is, let me first show you the calculations that are required; then I will explain them.
We are mixing two ingredients with sugar percentages 1% and 79% to obtain a mixture of 66% sugar. Here are all the calculations needed:
79-66 = 13;
66-1 = 65.
65:13 = 5:1.
(5/6)*120 = 100; (1/6)*120 = 20.
Answer: 100 ml of drink B and 20ml of drink A.
Here is the explanation of the calculations....
79-66=13 tells us how far the percentage of the mixture is from the percentage of drink B.
66-1=65 tells us how far the percentage of the mixture is from the percentage os drink A.
The ratio of those two differences is 65:13, or 5:1. That means the two ingredients must be mixed in the ratio 5:1 -- i.e., one ingredient is 5/6 of the mixture and the other ingredient is 1/6 of the mixture.
Since the percentage of the mixture is closer to drink B than to drink A, the larger portion of the mixture has to be drink B.
So to make 120 ml of the mixture, the amount of drink B needed is (5/6) of 120 = 100 ml; the amount of drink A needed is (1/6) of 120 = 20 ml.
|
|
|
