.
The six angles measures are 2x, 3x, 4x, 5x, 6x and 7x, where x is their common measure.
The sum of interior angles of any n-sided polygon is (n-2)*180 degrees, therefore
2x + 3x + 4x + 5x + 6x + 7x = 4*180, or
27x = 720
x = 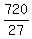 =
= 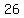
 degrees.
The greatest angle measure is 7 times
degrees.
The greatest angle measure is 7 times 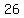
 degrees, or
degrees, or 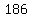
 degrees =
degrees = 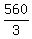 degrees.
degrees.
Solved.