SOLUTION: the height in cm of a candle is a linear function of the amount of time(hours) its been burning. When graphed, the function gives a line with a slope of -0.6. Suppose the height of

Click here to see ALL problems on Linear Equations And Systems Word Problems

Question 1119236: the height in cm of a candle is a linear function of the amount of time(hours) its been burning. When graphed, the function gives a line with a slope of -0.6. Suppose the height of the candle after 17 hours is 17.8 cm what was the height of the candle after 10 hours?
Answer by ikleyn(52798)   (Show Source):
You can put this solution on YOUR website!
.
the height in cm of a candle is a linear function of the amount of time(hours) its been burning.
When graphed, the function gives a line with a slope of -0.6. Suppose the height of the candle after 17 hours is 17.8 cm
what was the height of the candle after 10 hours?
~~~~~~~~~~~~~~~~~~~~~~~~~

            After reading the condition I have a question:   "10 hours" after WHAT ?

            I will interpret the question in this way:   "what was the height of the candle after 10 hours from the beginning ?"

Solution

1.   The common sense solution

The condition says that the candle looses 0.6 cm of its height each hour when it is burning. After 17 hours the candle was 17.8 cm long. Hence, after 10 hours from the beginning it was 17.8 + 7*0.6 = 17.8 + 4.2 = 22 cm.

2.   The formal solution

You have a straight line with the slope of -0.6 passing through the point (x,y) = (17,17.8). They ask to determine the value of the linear function at x = 10. Use the formula = 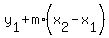, where m = -0.6 (the slope), = 10, = 17.8, = 10, = 17. = 17.8 - 0.6*(10-17) = 17.8 - 0.6*(-7) = 17.8 + 0.6*7 = 22 cm. You get the same answer as in the solution 1.