.
In your original equation
x^2 - y^2 = 2xy
divide both sides by y^2. You will get
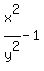 =
= 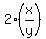 , or
, or
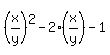 = 0.
In the last equation, introduce new variable t =
= 0.
In the last equation, introduce new variable t =  . Then the equation takes the form
t^2 - 2t - 1 = 0.
Apply the quadratic formula:
. Then the equation takes the form
t^2 - 2t - 1 = 0.
Apply the quadratic formula:
 =
= 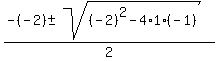 =
= 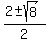 =
= 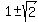 .
Since t = x/y and x > 0, y > 0, only positive root t =
.
Since t = x/y and x > 0, y > 0, only positive root t =  works and gives the
Answer.
works and gives the
Answer.  =
=  .
.
Solved.