Question 1118952: Hi can you help me solve this problem please?
"Coco has a jar containing pennies and nickels that add up to a total of $9.20. If she could switch the number of pennies with the number of nickels, there would be $26.80 worth of coins in the jar. How many pennies and nickels are in the jar?"
Can you show the step by step solving progress for their problem? Thanks.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52805)   (Show Source):
You can put this solution on YOUR website! .
Let P the number of pennies and N be the number of nickels in the jar.
Then the coins worth is P + 5N cents and the equation is
P + 5N = 920 (1) (cents)
Now, under the "if" scenario, it would be P nickels and N pennies, that would worth 5P + N cents. So, the second equation is
5P + N = 2680 (2) (cents)
Thus you have this system of two equation in 2 unknowns
P + 5N = 920 (1)
5P + N = 2680 (2)
To solve it, from eq(1) express P = 920-5N, and then substitute it into eq(2), replacing P. You will get a single equation for only one unknown N:
5*(920-5N) + N = 2680.
Simplify and solve for N:
4600 - 25N + N = 2680.
-24N = 2680 - 4600
-24N = -1920 ====> N = 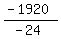 = 80.
Thus there are 80 nickels in the original collection.
Then the number of pennies is P = 920 - 5N = 920 - 5*80 = 920 - 400 = 520.
Solved.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! let n = number of nickels.
let p = number of pennies.
the number of cents in a nickel is 5.
the number of cents in a penny is 1.
the number of cents in a dollar is 100.
your first equation is 5n + p = 920.
if you switch the number of nickels with the number of pennies, then your second equation is 5p + n = 26.80.
re-arrange the variables so that your second equation reads n + 5p = 2680.
you have 2 equations that need to be solved simultaneously.
they are:
5n + p = 920
n + 5p = 2680
multiply the second equation by -5 to get:
5n + p = 920
-5n - 25p = -13400
add the 2 equations together to get:
-24p = -12480
solve for p to get:
p = 520.
in the first original equation of 5n + p = 920, replace p with 520 to get:
5n + 520 = 920
solve for n to get:
n = (920 - 520) / 5 = 80
replace n with 80 and replace p with 520 in both original equations to get:
5n + p = 920
n + 5p = 2680
become:
5*80 + 520 = 920
80 + 5*520 = 2680.
your solution is confirmed to be good.
it is:
number of nickels is 80 and number of pennies is 520 to get a total of 920 cents which is equal to $9.20.
number of nickels is 520 and number of pennies is 80 to get a total of 2680 cents which is equal to 26.80.
|
|
|
