Question 1118948: A community bird-watching society makes and sells simple bird feeders to raise money for its conservation activities. The materials for each feeder cost $5, and the society sells an average of 30 feeders per week at a price of $9 each. The society has been considering raising the price, so it conducts a survey and finds that for every dollar increase, it loses 3 sales per week.
(a) Find a function P that models weekly profit in terms of price per feeder. (Let x be the price per feeder.)
(b) What price should the society charge for each feeder to maximize profits?
(c) What is the maximum weekly profit?
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A community bird-watching society makes and sells simple bird feeders to raise money for its conservation activities.
The materials for each feeder cost $5, and the society sells an average of 30 feeders per week at a price of $9 each.
The society has been considering raising the price, so it conducts a survey and finds that for every dollar increase, it loses 3 sales per week.
(a) Find a function P that models weekly profit in terms of price per feeder. (Let x be the price per feeder.)
* * * As the problem is worded, it is much easier to me to use x for the exceed the price over 9 dollars. * * *
>>> I don't like VERY MUCH when somebody comes for help and starts teach me how to solve the problem.
>>> Especially when your advice makes the solution harder . . .
>>> Let me decide how to do it better - or solve the problem on your own . . .
The phrase " . . . for every dollar increase, it loses 3 sales per week." means that at the price (9+x) dollars the number of sales is (30-3x) feeders per week.
In turn, it means that the profit function per week as the function of x is
P(x) = (9+x)*(30-3x) - 5*(30-3x) (1) (profit = revenue minus cost)
It is the answer to question (a).
(b) What price should the society charge for each feeder to maximize profits?
All you need is to simplify (1) and find the maximum of this quadratic function:
P(x) = 270 + 30x - 27x - 3x^2 - 150 + 15x = -3x^2 + 18x + 120.
For a quadratic function q(x) = ax^2 + bx + c with negative leading coefficient "a" the maximum is achieved at x =  .
In your case a = -3, b = 18, so x = .
In your case a = -3, b = 18, so x = 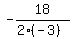 = 3.
So, the optimal price is 9+3 = 12 dollars per feeder.
(c) What is the maximum weekly profit?
The current weekly profit is 30*$9 - 30*5 = 120 dollars.
The projected (predicted) weekly profit is (see formula (1) )
(9+3)*(30-3*3) - 5(30-3*3) = 147 dollars. = 3.
So, the optimal price is 9+3 = 12 dollars per feeder.
(c) What is the maximum weekly profit?
The current weekly profit is 30*$9 - 30*5 = 120 dollars.
The projected (predicted) weekly profit is (see formula (1) )
(9+3)*(30-3*3) - 5(30-3*3) = 147 dollars.
Solved.
---------------
If you want to see other similar solved problems, look into the lesson
- Using quadratic functions to solve problems on maximizing revenue/profit
in this site.
My other lessons in this site on finding the maximum/minimum of a quadratic function are
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|