|
Question 1118783:
Problema Solution
A Broadway theater has 700 seats, divided into orchestra,main and balcony seating. Orchestra seats sell for $40, main seats sell for $25, and balcony seats for $20. If all the seats are sold, the gross revenue to the theater is $18,400. If all the main and balcony seats are sold, but only half the orchestra seats are sold, the gross revenue is $15,600. How many are there of each kind of seat?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52756)   (Show Source):
You can put this solution on YOUR website! .
After reading the condition, you should notice momentarily that half of the orchestra seats costs 18400 - 15600 = 2800 dollars.
Hence, the half of the orchestra seats is  = 70 seats, and the entire number of the orchestra seats is 2*70 = 140.
Thus you just can reduce the original problem to the simpler one:
There are 700-140 = 560 seats; of them, main seats sell for $25 and balcony seats sell for $20.
The revenue obtained for main seats and balcony seats is 18400 - 140*40 = 12800 dollars.
You can solve this problem as an two-unknown problem or even as an one-unknown problem, on your choice.
I prefer one-unknown, as it is shown below.
Let x be the number of main seats.
Then the number of balcony seats is (560-x).
The money equation for this reduced problem is
25x + 20*(560-x) = 12800 dollars.
Simplify and solve for x:
25x + 20*560 - 20x = 12800
25x - 20x = 12800 - 20*560 = 1600
5x = 1600 ====> x = 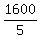 = 320.
Answer. 140 orchestra seats, 320 main seats and (560-320) = 240 balcony seats.
Solved.
Answer by greenestamps(13196)  (Show Source):
You can put this solution on YOUR website!
As tutor @ikleyn pointed out, you want to simplify the problem immediately by seeing that the $2800 difference in revenue is due to the fact that only half of the $40 orchestra seats were sold; some quick calculations show that the number of orchestra seats is 140, bringing in a total revenue, if all are sold, of $5600. Then if all the seats are sold, that leaves 560 seats combined for the $20 seats and $25 seats, bringing in total revenue of $18400-$5600=$12800.
From there I prefer a different method than the traditional algebraic solution she uses. Here is one way of explaining the method I like to use on this kind of problem.
If all the remaining 560 seats were $25 seats, the revenue would be $14000; if all were $20 seats, the revenue would be $11200.
Where the actual remaining revenue of $12800 lies between those two figures of $14000 and $11200 exactly determines the ratio of $25 seats to $20 seats.
$14000-$12800 = $1200; $12800-$11200 = $1600.
$1200:$1600 = 3:4
Since the actual remaining revenue is closer to $14000 than to $11200, the larger number of seats must be the $25 seats.
A 3:4 ratio then means 4/7 of the remaining 560 seats are $25 seats and 3/7 of them are $20 seats.
$25 seats: (4/7)*560 = 320
$20 seats: (3/7)*560 = 240
Final answer: 140 $40 seats, 320 $25 seats, 240 $20 seats.
|
|
|
| |
