.
Consider complex number
z =  . (1)
It is the root of the degree 7 of 1 in complex domain, so
. (1)
It is the root of the degree 7 of 1 in complex domain, so
 = 1 =
= 1 = 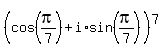 . (2)
Apply the binomial decomposition to get
1 =
. (2)
Apply the binomial decomposition to get
1 =  +
+ +
+ +
+ +
+ +
+ +
+  +
+ .
In the last equation extract the imaginary part, which is equal to zero:
0 =
.
In the last equation extract the imaginary part, which is equal to zero:
0 =  +
+  +
+  +
+  .
Replace the degrees of "i" by i with the corresponding signs and then divide both sides by
.
Replace the degrees of "i" by i with the corresponding signs and then divide both sides by  . You will get
0 =
. You will get
0 =  -
-  +
+  -
-  .
Divide by
.
Divide by  both sides. You will get
both sides. You will get
 -
-  +
+  - 7 = 0. (3)
Thus you see that
- 7 = 0. (3)
Thus you see that  is the root of the polynomial equation
is the root of the polynomial equation
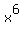 -
-  +
+  - 7 = 0. (4)
If you do the same starting from z =
- 7 = 0. (4)
If you do the same starting from z = 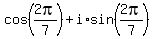 instead of z =
instead of z =  , you will get by the same way that
, you will get by the same way that
 is the root of the same polynomial equation.
Similarly, If you do the same starting from z =
is the root of the same polynomial equation.
Similarly, If you do the same starting from z = 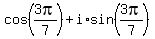 instead of z =
instead of z =  , you will get by the same way that
, you will get by the same way that
 is the root of the same polynomial equation.
. . . and so on . . .
Thus, the six numbers
is the root of the same polynomial equation.
. . . and so on . . .
Thus, the six numbers  ,
,  ,
,  , . . . ,
, . . . ,  all are the roots of the equation (4).
Then, according to Vieta's theorem, the product of the roots is equal to the constant term:
all are the roots of the equation (4).
Then, according to Vieta's theorem, the product of the roots is equal to the constant term:
 .
. .
. . . . . .
. . . . .  = -7.
Now take into account that
= -7.
Now take into account that  = -
= - ,
,  = -
= - and
and  = -
= - .
Based on it, you get
.
Based on it, you get
 .
. .
. = 7,
which implies
= 7,
which implies
 .
. .
. =
=  .
It is exactly what has to be proved.
.
It is exactly what has to be proved.
********************
* * * SOLVED. * * *
********************