Question 1118550: An experiment consists of two independent trials. The outcomes of the first trial are A, B, and C, with probabilities of occurring equal to 0.5, 0.3, and 0.2, respectively. The outcomes of the second trial are E and F, with probabilities of occurring equal to 0.3 and 0.7. Draw a tree diagram representing this experiment. Use this tree diagram to find the probabilities below.
(a) P(B)
(b) P(F | B)
(c) P(B intersection F)
(d) P(F)
Answer by Theo(13342)   (Show Source): (Show Source):
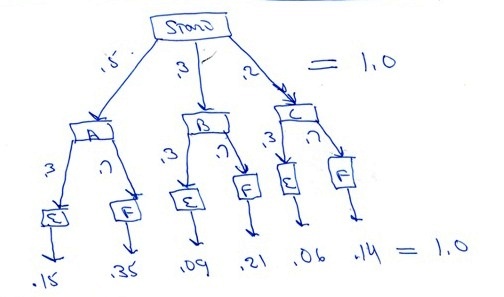
You can put this solution on YOUR website! you have 3 branches to start with.
they are A,B,C
p(A) = .5
p(B) = .3
p(C) = .2
the second trial happens after the first.
the outcomes of that trial are:
p(E) = .3
p(F) = .7
p(B) stays the same at .3
p(F and B) = p(F) * p(B) = .7 * .3 = .21
p(F given B) = p(F and B) / p(B) = .21 / .3 = .7
here's what my tree diagram looks like.
since the events are independent, p(F and B) is equal to p(F) * P(B).
since the events are independent, p(F given B) is equal to p(F).
|
|
|