Question 1118534: How many ounces each of a 20% acid solution and a 50% acid solution must be mixed together to get 120 ounces of a 30% solution acid?
Found 3 solutions by Alan3354, ikleyn, greenestamps:
Answer by Alan3354(69443)   (Show Source):
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
Let x be the amount of the 20% solution to mix.
Then the amount of the 50% solution is (120 - x) ounces, and as soon as you mix these amounts, you will automatically provide
120 ounces of the resulting mixture.
So, the only thing to care is to provide the required concentration of the mixture.
x ounces of the 20% solution contain 0.2x ounces of the pure acid.
(120-x) ounces of the 50% solution contain 0.5*(120-x) ounces of the pure acid.
Finally, 120 ounces of the 30% solution contain 0.3*120 ounces of the pure acid.
So, your balance equation is
0.2x + 0.5*(120-x) = 0.3*120.
It is your basic equation, and as soon as you got it, the setup is completed.
To solve the equation, simplify it step by step
0.2x + 0.5*120 - 0.5*x = 0.3*120
-0.3x = 0.3*120 - 0.5*120
-0.3*x = -0.2*120
0.3*x = 0.2*120 ====> x = 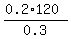 =  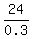= 80.
Answer. 80 ounces of the 20% acid should be mixed with 120-80 = 40 ounces of the 50% acid solution.
Solved.
-----------------
It is a standard and typical mixture word problem.
There is entire bunch of introductory lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn has shown a solution using the usual algebraic method; she has also pointed you towards several other examples of similar problems which use the same method.
It is of course useful to know that method. However, there is a much faster and easier way to find the answer to ANY mixture problem like this where two "ingredients" are being mixed.
For your problem, here is the entire set of calculations required:
(1) 50-30 = 20; 30-20 = 10
(2) 20:10 = 2:1
(3) 2 parts 30% acid to 1 part 50% acid
(4) 2/3 of 120 ounces = 80 ounces of 30% acid; 1/3 of 120 ounces = 40 ounces of 50% acid
It's even faster if you think in terms of what those calculations mean. Here is the way I think of it:
"The 30% target is twice as close to 20% as it is to 50% (step (1) above); therefore the solution must use twice as much of the 20% ingredient as the 50% ingredient (step (2) above). A 2:1 ratio with a total of 120 ounces means 80 ounces of 20% and 40 ounces of 50% (steps 3 and 4 above)."
|
|
|
