SOLUTION: How do I go about solving this math problem? In a triangle, ΔABC the segment AM is the median to BC. Let D be the midpoint of AM and let N be the point on AC such that the

Algebra ->  Triangles -> SOLUTION: How do I go about solving this math problem? In a triangle, ΔABC the segment AM is the median to BC. Let D be the midpoint of AM and let N be the point on AC such that the       Log On


   

Question 1118483: How do I go about solving this math problem?
In a triangle, ΔABC the segment AM is the median to BC. Let D be the midpoint of AM and let N be the point on AC such that the points B, D, and N are on the same line. Find the ratio of DN to DB.

Found 3 solutions by greenestamps, math_helper, ikleyn:
Answer by greenestamps(13210) About Me  (Show Source):
You can put this solution on YOUR website!


The ratio of DN to DB is 1:3.

I think I have seen this problem before, or a very similar problem. It seemed to me after looking at the problem for only a short time that the answer should be 1:3; but I have been unable to come up with a general proof.

I think a proof can be made using the areas of triangles. With D the midpoint of AM and M the midpoint of BC, there are a lot of triangles for which the ratio of the areas is easy to determine. But I haven't been able to put the complete formal general proof together.

So let's use a powerful problem solving concept to show the answer is 1:3.

The problem does not say anything about what kind of triangle it is; that means the answer is going to be the same for ANY triangle. So choose a triangle with which coordinate geometry will let you find the answer easily.

That is a very useful technique in solving many similar geometry problems. If the statement of a problem says that a certain conclusion can be made without precisely defining a figure, then the conclusion should be able to be made using ANY figure that satisfies the general statement of the problem.

For your problem the special case I used (after playing around with a few possibilities) is A(0,2), B(0,0), and C(4,0); that makes M(2,0); and that makes D(1,1).



Now use the equations of lines BD and AC to find the coordinates of point N; then it will be easy to find the ratio of DN to DB.

BD: y=x
AC: y+=+%28-1%2F2%29x%2B2
x+=+%28-1%2F2%29x%2B2
%283%2F2%29x+=+2
x+=+4%2F3

The x coordinate of N is 4/3; since it is on the line y=x, the y coordinate is also 4/3.

Then from B to D is 1 unit in each the horizontal and vertical directions; and from D to N is 1/3 unit in each direction. That means BD is 3 times the length of DN -- i.e., the ratio of DB to DN is 1:3.

Proof complete.

Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
The answer is 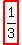+highlight%281%2F3%29+

This is admittedly a long procedure so there may very well be shorter ones. I'm confident the answer is correct as I tried it with a sample triangle and it works.

There are a lot of algebraic steps, so I will just outline the procedure.
Draw the triangle ABC such that A and B lie on the x-axis. So triangle ABC has the following vertices:
A@ (0,0)
B@ (Bx, 0) <— notation is B sub x = x coordinate of B, sorry it can look a little confusing
C@ (Cx,Cy)

Point M is then at ((Bx+Cx)/2, Cy/2)
Point D is at ((Bx+Cx)/4, Cy/4)
1. Find the equation of line BD. You will find it is y = (Cy/(Cx-3Bx))x - (Bx*Cy)/(Cx-3Bx)
2. Find the equation of line AC. You will find it is y = (Cy/Cx)x
3. Set these two equations equal to each other to find Nx (where N is at (Nx, Ny))
4. Once Nx is found, plug in to (2) to find Ny. You should find N to be at (Cx/3, Cy/3)
6. Write equations for |DN| and |DB|
|DN| = [ ((Cx+Bx)/4 - (Cx/3))^2 + (Cy/4 - Cy/3)^2 ] ^(1/2)
:
|DN| = [ ( 9Bx^2 - 6BxCx + Cx^2 - Cy^2 ) / 144 ] ^(1/2)


|DB| = [ ((Cx - 3Bx)/4 )^2 + (Cy/4)^2 ]^(1/2)
:
|DB| = [ (9Bx^2 - 6BxCx + Cx^2 + Cy^2) / 16 ] ^(1/2)
Writing |DN| / |DB| and bringing everything under the radical sign, allows all the variables to cancel, leaving only:
( 16/144 ) ^(1/2)
= ( 4/12 )
= (1 / 3 )





——————————————————————
I started with the same method as @greenestamps. I used a special case and worked it out numerically, and then I generalized it. The proof must be done using a general case, not a special case.


Also note that |DN| / |DB| = [AND] / [BMD] where [T] denotes area of triangle T
which can be shown by making use of A = (1/2)b*h (h = side*sin(alpha)), vertical angles are equal, and these relationships that arise from properties of medians:
[ACM] = [ABM] = (1/2)[ABC]
[ABD] = [BMD] = (1/2)[ABM] = (1/4)[ABC]
—————————
6/16: Yes, tutor @ikleyn's solution is most appropriate (geometric). I wish I had seen that construction.

Answer by ikleyn(52897) About Me  (Show Source):
You can put this solution on YOUR website!
.
It is a Geometry problem,  and a Geometric solution is expected.  It is presented below. 

Figure 1 shows what is given. Figure 2 shows an extended plot.


 
  

  



  Figure 1. Given data 
 
  



  Figure 2. Extended plot
  
  




In Figure 2,  the triangle ABC is extended to the parallelogram ABEC;  the median AM is extended to the diagonal of the parallelogram.

Draw the line CP parallel to BN; the point F is its intersection with the diagonal AE.


Then the triangles  DBM  and  FCM are congruent by  ASA-test;  hence,  DM is congruent to MF.


Next, triangles ADN and AFC  are similar, and AF is three times AD.

Hence, the similarity coefficient is 3:1 from the larger to the smaller.

Hence,  CF  is three times ND.


It means that ND is %281%2F3%29 of DB.

Solved.