Question 1118481: What is the probability that there are at least two people with the same birthday in a class of 40?
Found 2 solutions by Shin123, math_helper:
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of possible incomes is 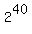 which is 1,099,511,627,776. There is 41 incomes that does not favor the probability we want to get. So 1,099,511,627,776-41=1,099,511,627,735. Therefore, the probability is which is 1,099,511,627,776. There is 41 incomes that does not favor the probability we want to get. So 1,099,511,627,776-41=1,099,511,627,735. Therefore, the probability is 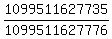 which is approx. 99.9999999962711% which is approx. 99.9999999962711%
Answer by math_helper(2461)   (Show Source): (Show Source):
|
|
|